Die Welt ist Klang

Die Mythen der Völker haben es schon immer gewußt: Gott erschuf die Welt aus dem Klang, aus der Musik. Überall auf der Welt findet man Schöpfungslegenden, bei denen die Musik maßgeblich an der Entstehung der Welt beteiligt war. “Am Anfang war das Wort”, heißt es im Johannesevangelium. Ein gesprochenes Wort aber ist ein Klang. Harmonik, griech. harmonikos, heißt “zur Musik gehörig”. Die Harmonikale Forschung geht aber weit über die “Harmonielehre” der Musik hinaus, sie ist vielmehr die Kunde von der uralten Lehre vom Klang der Welt.

“Gott machte eine Statue aus Ton. Er formte den Ton nach seinem Bilde. Er wollte, dass die Seele in diese Statue eingehe. Aber die Seele wollte nicht gefangen sein. Denn es liegt in ihrer Natur, dass sie fliegend ist und frei. Sie will nicht begrenzt und gebunden sein. Der Körper ist ein Gefängnis, und die Seele wollte dieses Gefängnis nicht betreten. Da bat Gott seine Engel, Musik zu spielen. Und als die Engel spielten, wurde die Seele ekstatisch bewegt. Sie wollte die Musik noch klarer und unmittelbarer erfahren, und deshalb betrat sie den Körper. ” Hafiz sagt: “Die Leute sagen, dass die Seele, als sie dieses Lied hörte, den Körper betrat. Aber in Wirklichkeit war die Seele selbst das Lied.”

(Überlieferung von Hafiz, einem der großen Poeten des alten Persiens.
Man beachte die Doppeldeutigkeit des Wortes “Ton”!)

 

Die Harmonikale Forschung geht zurück auf Pythagoras, auf die Zeit 600 v. Chr. Er fand durch Experimente an einem einseitigen Instrument, dem Monochord, heraus, dass es einen eindeutigen Zusammenhang gibt zwischen Zahlen und Tönen, also zwischen Quantität und Qualität, zwischen Wellen- bzw. Saitenlängen und Tönen, letztlich zwischen Verstand und Gemüt, Materie und Seele. Die Zahlen beginnen zu tönen, die Materie wird beseelt: Abb.1

Pythagoras neue Einsicht in die Struktur der Musik war eine Quelle für das wissenschaftliche Denken der alten Griechen und beeinflusste ihre Kultur nachhaltig. Er sah die Beziehung zwischen Ton und Zahl in beide Richtungen:

1. Die Rückführung des Qualitativen auf das Quantitative:
Beispiel: “Aha, das klingt so, weil es eine bestimmte Proportion hat.” Eine Erklärung der Qualität war eine völlig neue Idee und verschaffte eine Orientierung innerhalb der mythologisch und symbolisch übervollen Welt der griechischen und vorklassischen Menschen. Diese Weltsicht wurde zum Fundament der modernen abendländischen Wissenschaft. Aber Pythagoras dachte auch andersherum:

2. Die Bewertung des Quantitativen (Zahl, alles Materielle) durch das Qualitative war ihm genauso wichtig. Beispiel: “Die Proportion ist dann gut, wenn sie meine Seele anrührt, wenn sie ‘schön’ ist. ” Diese Seite ist seit der Antike immer mehr vergessen worden. Wissenschaft und Technik haben sich von der Seele des Menschen gelöst und verselbständigt.

“Am Anfang herrschte das Dunkel. Amaterasu, die Göttin der Sonne, thronte noch nicht am Himmel. Sie lebte in einer Hohle. Die Welt war kalt und unwirtlich und ohne Leben.

Da nahm Gott sechs riesige Bögen, band sie zusammen und schuf auf diese Weise die erste Harfe. Auf ihr spielte er wunder- schöne Melodien. Von ihnen angelockt, erschien die reizende Nymphe Ameno-Uzume. Hingerissen von der Harfenmusik begann sie zu tanzen – und schließlich auch zu singen. Die Sonnengöttin Amaterasu wollte die Musik, die von ferne zu ihr drang, besser vernehmen. Deshalb schaute sie aus ihrer Höhle hervor, und im gleichen Moment erstrahlte die Welt im Licht. Die Sonne wurde sichtbar und spürbar – und Blumen und Pflanzen und Baume begannen zu wachsen. Und Fische und Vögel, Tiere und Menschen betraten die von Licht erfüllte Erde. Die Götter aber beschlossen, fortan Gesang und Tanz zu pflegen, damit die Sonnengöttin nie mehr in ihre Höhle zurückkehrte, denn sie wussten:

Es war zwar die Sonne, durch die das Leben begonnen hatte, aber ohne die Harfenmusik der sechs großen Bögen und ohne den Gesang der Nymphe Ameno-Uzume hätte sich Amaterasu, die Göttin der Sonne, nie auf ihrem himmlischen Thron niedergelassen. Sie wäre ewig in ihrer Höhle geblieben. Und also war es der Klang, waren es Musik und Tanz, mit denen die Welt begann. “

(Schöpfungslegende aus Japan.)

 

Die Sonne beginnt zu leuchten, weil Musik ertönt, so die japanische Legende. Jetzt hat auch die Sonoluminiszens, ein moderner Wissenschaftszweig, herausgefunden, dass aus Klang Licht entstehen kann: Wenn man eine Luftblase im Wasser hochfrequentem Schall (30.000 Hz) aussetzt, dann beginnt sie, Lichtblitze abzuschicken, wobei Temperaturen entstehen wie an der Sonnenoberfläche. Durch den Schall wird die Luftblase auch im Wasser in ihrer Lage gehalten.

Wer war Pythagoras?
Pythagoras wurde um 570 v. Chr. auf der Insel Samos geboren. Als der Tyrann Polykrates diktatorisch die Macht übernahm, verließ er die Insel und unternahm ausgedehnte, langjährige Reisen. In Ägypten wurde er in die Geheimnisse der Priesterlehre eingeweiht. Von dort stammt wahrscheinlich auch der nach Pythagoras benannte Lehrsatz: a2 + b2 = c2. Fussnote 1

Mit 40 Jahren ließ sich Pythagoras im unteritalienischen Kroton nieder und wurde zum Mittelpunkt des so genannten pythagoräischen Bundes. Als Gelehrter hatte er einflussreiche Anhänger. Dennoch kamen sie in den Verdacht staatgefährdender Umtriebe und wurden verfolgt. Bei einem Attentat auf eine Versammlung der Pythagoräer soll Pythagoras mit 40 seiner Anhänger verbrannt worden sein. Die Macht des Bundes war zerbrochen, es ist aber anzunehmen, dass seine Lehre noch jahrhundertelang in geheimen Kreisen weitergegeben wurde.

Was hat Pythagoras gelehrt?
Der pythagoräische Geheimbund in Kroton war aufgebaut nach dem Vorbild der ägyptischen Mysterienschulen und lehrte eine streng behütete “Theologie in Gestalt von mathematischen Figuren”. Von Pythagoras selbst gibt es keine als echt erachteten Überlieferungen, wohl aber von seinen Schülern. Einige dieser verschlüsselten Sätze oder Theoreme möchte ich hier ihrer Schönheit wegen zitieren:

1. “Die ganze Welt ist nur eine Harmonie und Zahl”. (Aristoteles)
2. “Nichts von Trug nimmt die Natur der Zahl und der Harmonie in sich auf, denn er ist ihnen nicht eigen.” (Philolaisches)
3. “Die Harmonie ist bunt gemischter Dinge Einigung und verschieden gestimmter Zusammenstimmung. Sie ist ganz aus Entgegengesetztem entstanden. “
4. “Aus Begrenzendem und Unbegrenztem ist die Welt und alles in ihr zusammen gefügt.”
5. “Über der Grenze jedoch und dem Unbegrenzten steht als Urgrund dieser beiden Urgründe der gewordenen Dinge, als nicht gewordene Ursache der Ursachen: Gott.”

Wie kamen die Pythagoräer zu solchen Aussagen, die sie noch dazu alle aus den Gesetzen der Musik, bzw. Mathematik heraus entwickelt haben wollen?

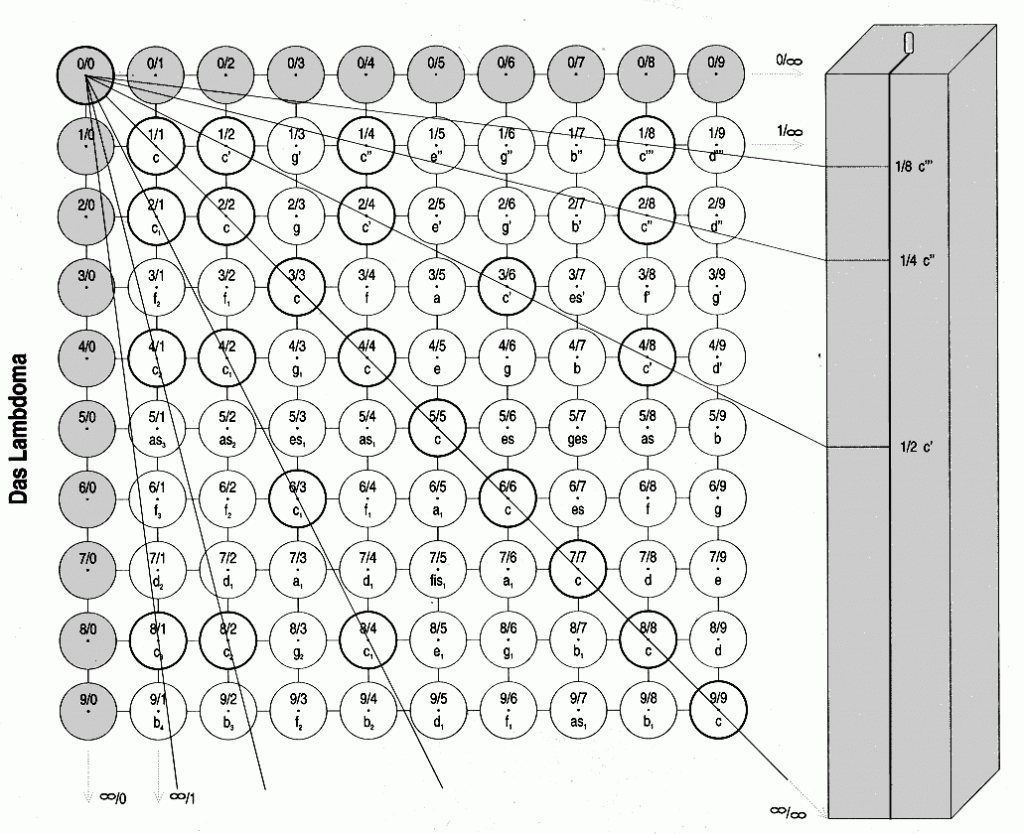
Das Kernstück der pythagoräischen Lehre war die pythagoräische Tafel, das Lambdoma, das vor etwa 130 Jahren von A. Thimus wiederentdeckt und rekonstruiert wurde. Ursprünglich wurde die Tafel in Form des griechischen Buchstabens Lambda dargestellt, woher es auch seinen Namen bekam. Das Lambdoma ist mathematisch streng gesetzmäßig aufgebaut: Abb.2

1. waagrecht bleibt der Zähler konstant und der Nenner geht gegen “Unendlich”, d.h. die Brüche werden immer kleiner, gehen gegen den Grenzwert Null, werden Null aber nie erreichen.
2. senkrecht bleibt der Nenner konstant und der Zähler geht gegen Unendlich, die Zahlenwerte wachsen unbegrenzt gegen Unendlich an.
3. die Diagonale ergibt überall den Wert 1.
4. Den Punkt 0/0 erhalten wir durch die Rückwärtsverfolgung der beiden äußeren Reihen, sowie die Rückwärtsverfolgung der Diagonale in logisch einwandfreier Weise.

Wir wissen bereits, dass jede Proportion ganzer Zahlen sich als ein Tonintervall darstellen lässt. Legen wir für 1/1 den Grundton c fest, dann ergibt sich bei 1/2 das c’, bei 1/3 das g’ usw. Daraus folgt:

1. waagrecht entstehen lauter Obertonreihen
2. senkrecht lauter Untertonreihen (d.h. die Intervalle der Obertonreihe spiegeln sich nach unten.) 2: 1 bedeutet doppelte Saitenlänge, d.h. der Ton klingt eine Oktave tiefer, die Frequenz halbiert sich. In der Natur sind bisher noch keine Untertöne nachgewiesen worden, mathematisch lassen sie sich jedoch mit verblüffender Gesetzmäßigkeit ableiten.
3. Auf jedem Ton der Obertonreihe bildet sich eine Untertonreihe und auf jedem Ton der Untertonreihe bildet sich eine Obertonreihe.
4. Waagrecht entstehen an 3., 4. und 5. Stelle Durdreiklänge.
5. Senkrecht entstehen an 3., 4. und 5. Stelle Molldreiklänge
6. Der Ausgangston c zieht sich als Diagonale durch das Diagramm. Alle Töne oberhalb sind höher als c, alle Töne unterhalb sind tiefer als c.
7. Alle gleichen Töne (gleiche Proportionen) liegen auf einer Geraden.
8. Alle diese Geraden laufen strahlenförmig in einem Punkt zusammen, dem Punkt 0/0.

Gleiche Tonwerte wiederholen sich, aber immer in einer anderen Umgebung. Je weiter sie sich vom Ursprung entfernen, umso schillernder und vielfältiger wird ihre Umgebung.

Den Pythagoräern galt das als Hinweis auf die Reinkarnation. Alle Gleichtonlinien laufen im Punkt 0/0 zusammen, in dem Punkt, der hinter allem liegt, der sich nicht materialisiert: das höchste Schöpfungsprinzip, die Ursache der Ursachen, Gott. (Re-ligio = zurückverfolgen). Die Gleichtonlinien laufen nicht im Punkt I / 1 zusammen, wie man denken könnte, denn es war ja der Ausgangspunkt und Grundton unserer Tonreihen, der materielle, irdische Schöpfungspunkt, Vater und Mutter, sondern im dem nichtmateriellen 0/0. Der Punkt 0/0 ist mathematisch gesehen alles wie auch nichts. Er enthält alles in sich, lässt sich aber durch nichts mehr ausdrücken. 0/0 ist durch keinen zugänglichen Begriff fassbar. Den Pythagoräern war er Symbol für Gott, die Kabbalisten sprechen von “En-Sof”, dem Abstrakten, dem Absoluten, der Uridee, Jakob Böhme vom Urgrund, Teilhard de Chardin nannte ihn den Punkt Omega.

Es gibt keinen Gott außerhalb von uns, noch gibt es keinen Gott. 0/0 ist in allem enthalten, d.h. alles ist eine ganz spezielle Ausprägung von 0/0. Andersherum erhält 0/0 seine Existenz erst durch die materielle, hörbare Welt, ohne sie bleibt er ein Gedankenkonstrukt.

Die Aussagen und Schlussfolgerungen, die am Lambdoma gefunden werden können (für den Klang, für Schwingung) können auf alles Materielle übertragen werden, denn was wir mittlerweile mit Gewissheit über die Materie sagen können, ist, dass sie schwingt. Alle Elementarteilchen zerfallen bei weiterer Untersuchung in immer kleinere Teilchen. Was bleibt, ist Schwingung, Rhythmus, Energie. An dieser Grenze sprechen sogar manche Physiker von Liebe oder von Gott.

Im Herzen jedes Stückes Materie   liegt ein “Stützpunkt Gottes”.
Dasjenige innere Zentrum, durch das die Dinge zueinander streben.

(Teilhard de Chardin)

Aus der harmonikalen Werkstatt:
Neuere und ältere Untersuchungen haben gezeigt, dass die harmonikalen Gesetzmäßigkeiten nicht nur in der Musik und Mathematik auftreten, sondern auch in den Proportionen des Makrokosmos, des Mikrokosmos und unserer irdischen Welt. Überall überwiegen konsonante Zusammenklänge, also Proportionen aus niedrigen ganzen Zahlen. Hier eine Auswahl:

1. Spektrallinien
In einem Spektroskop zerfällt das Licht in farbige Bänder, die mit schwarzen Linien scharf voneinander abgegrenzt sind. Jedes chemische Element, jeder Fixstern hat sein eigenes charakteristisches Spektrum, das harmonikal gedeutet werden kann.

2. Astronomie
Schon die antiken Pythagoräer kannten den Gedanken einer akustischen “Sphärenharmonie”. Von Aristoteles kommt die Auffassung, dass die Planeten am Himmel Töne erzeugen, und zwar infolge ihres Umlaufs und der sich durch Distanz und Geschwindigkeit ergebenden Proportionen, welche musikalische sind. Durch die Wiederbelebung des antiken Gedankenguts in der Renaissance kamen die Gedanken der Pythagoräer zu einer zweiten Blüte. Johannes Kepler (1571-1630) war von Jugend auf von dem Gedanken der Weltharmonie begeistert und in seinem Werk “Harmonices Mundi” gelang ihm erstmalig der Nachweis von Musikgesetzen in den Planetenbahnen. Er entdeckte, dass die Planeten die Sonne auf elliptischen Bahnen umkreisen und ihre Geschwindigkeit im sonnennahen Perihel größer ist als im sonnenfernen Aphel. Er setzte diese Umlaufgeschwindigkeiten der Planeten untereinander in Beziehung und fand nur musikalische Intervalle. Es ergeben sich fast ausschließlich die Töne des Durdreiklangs! Natürlich kann man diese Töne nicht direkt hören, aber wir können sie auf dem Monochord einstellen, um sie erklingen zu lassen.

Francis Warrain ergänzte Keplers Untersuchungen 1940 um die Werte der neu gefundenen Planeten Uranus, Neptun und Pluto. Er konnte Keplers Werte bis auf den Messwert von Merkur bestätigen und fand bei allen 39 Proportionen vertraute musikalische Intervalle. Wenn wir alle Intervalle als Obertöne eines gemeinsamen Grundtones c auffassen, gehören mit Ausnahme von 4 Tönen alle der Durtonleiter an.

3. Kristalle
Kristalle sind nach Symmetriegesetzen aufgebaut, haben also einfachste Ordnungsprinzipien, die harmonikal gedeutet werden können. Diese Eigenschaften äußern sich bereits in der atomaren Struktur des Kristalls. Es gibt 32 Kristallklassen, denen jedes existierende Kristall zugeordnet werden kann. Drehung und Spiegelung sind die Hauptmethoden bei der Feststellung der Symmetrie. Es sind nur Drehungen um 360′,180′,120′,90′ und 60′ möglich, was der Bruchreihe 1/1, 1/2,1/3,1/4,1/6 entspricht (bei 1/1 = 360′), die harmonikal gedeutet werden kann (c, c’, g’, c”, g”).

Anfang unseres Jahrhunderts hat Victor Goldschmidt eine mathematische Formel für die Systematik gefunden, nach der Kristalle Flächen bilden. Die Tafel entspricht exakt dem phytagoräischen Lambdoma, das er nicht kannte, bis zu Zahl 4 bzw. 1/4!

4. Chemie
Die drei für das Leben wichtigsten chemischen Elemente, Wasserstoff, Kohlenstoff und Sauerstoff stehen bezüglich ihrer Kernladungen und Atomgewichte in einem sehr bemerkenswerten harmonikalen Verhältnis zueinander. Fasst man sie Zahlen als Partialtöne einer Obertonreihe auf, so ergeben sich zwei Zahlenreihen aus gleichen Tonwerten, nur in verschiedenen Oktavlagen. Und es zeigen sich die konsonantesten Grundintervalle Oktave und Quinte.

Wenn sich Atome zu Molekülen verbinden, streben sie höchste Symmetrie an und bilden sich gerne in den Formen der sog. 5 “Platonischen Körper” (Abb.3). Diese Körper wurden erstmals von Platon in seinem Dialog “Timaios” beschrieben und sind aus gleichen regelmäßigen Vielecken zusammengesetzt.

Diese Körper (es gibt übrigens nur diese fünf!) tönen, was das Verhältnis der Zahl ihrer Kanten und Flächen betrifft, hauptsächlich im Durdreiklang.

Die fünf Platonischen Körper

 

Von Links: Tetraeder, Hexaeder, Oktaeder,  Ikosaeder,  Dodekaeder

5. Botanik
Im Pflanzenreich taucht erstmals die Zahl fünf als morphologische Konstante auf, (die in der inneren Struktur der Kristalle noch fehlte). Es gibt z.B. Pflanzen mit fünf Blütenblättern, Staubgefäßen u.a. Die fünf entspricht der Terz der Obertonreihe, die auch der “Geschlechtston” in der Musik genannt wird, denn die Terz bestimmt über das Tongeschlecht. (Dur c-e-g = große Terz; Moll c-es-g = kleine Terz) Fussnote 2. Goethe fand heraus, dass die Töne der Tonleiter in Winkeln aufgezeichnet die Form eines Urblattes ergeben Abb. 3 – die Tonleiter birgt die Blattform in sich.

Das Universum und ich existieren zusammen, und alle Dinge und ich sind eins.
Da alle Dinge eins sind, ist kein Grund mehr zur Rede.
Da ich jedoch eben gesagt habe, daß alle Dinge eins sind,
wie kann da Rede nicht wichtig sein?
Hinter den Teilen ist immer etwas Ungeteiltes,
hinter dem Bestreitbarem etwas Unbestreitbares.
Du fragst: Was?
Der Weise trägt es in seinem Herzen.

(Dschuang-tse)

6. Baukunst – Architektur
Die alten Baumeister benutzten solche Proportionen, die untereinander in konsonierenden Intervallverhältnissen stehen, die also auch für unsere Seele wohltuend waren., v.a. den Dreiklang 1c, 3 g’, 5 c” und dessen Multiplikationen.

Die Harmonikale Forschung ist ein Baustein einer neuen, nachmaterialistischen Wissenschaft vom Leben. Wir sind nicht getrennt vom Kosmos, die Formen, die wir in uns tragen, kommen uns in der Natur entgegen.

Es gibt nur ein Sein.

Die Sprache der Musik ist universell. Die Natur kann nicht lügen. Sie kommuniziert direkt über die Aura, d.h. über feinstoffliche Schwingungen, Formen, Klänge. Musik- der Klang – ist die gemeinsame Seele aller Geschöpfe. Sie ist wie eine Informationsmatrix für Kommunikation mit allen Mitgeschöpfen, mit Pflanzen, Kristallen, mit Tieren. Bevor wir Musik machen, macht die Musik uns.

---

Quellenangaben:
Rudolf Haase: Der messbare Einklang. Grundzüge einer empirischen Weltharmonik. Klett, Stuttgart 1976

Joachim Ernst Berendt: Nada Brahma. Die Welt ist Klang. Insel 1983, Rororo 1990, und die gleiche Rundfunksendung, erhältlich bei 2001 Versand auf 4 CDs.

 

---

Abb.1. ←Zurück
Grundlagen für die, die es genau wissen wollen.
Teile ich eine Saite am Monochord mit dem Grundton C = 138 Hz genau in der Hälfte, dann erhalte ich einen Ton, der um eine Oktave höher liegt, c. Dieser Ton schwingt doppelt so schnell, d.h., er hat die doppelte Frequenz, 2x138Hz.

 

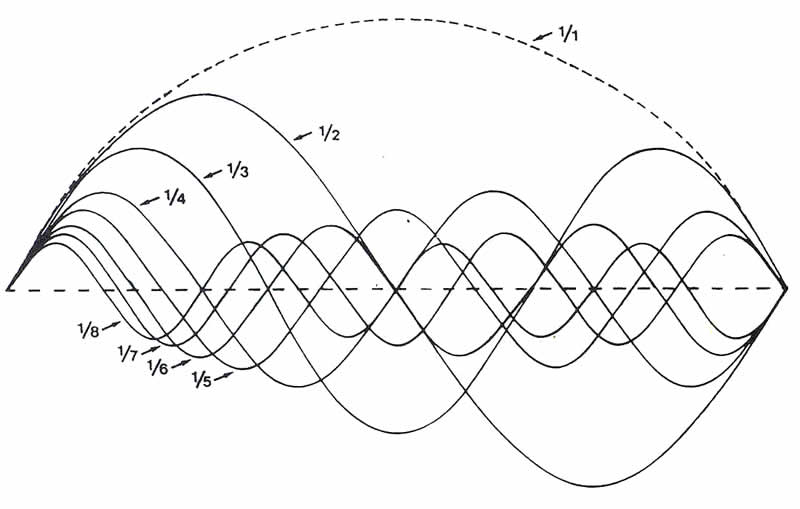
Bei einem Drittel der Saite erklingt ein g mit der Frequenz 3×138 Hz. Bei einem Viertel (die Hälfte der Hälfte) erklingt wieder ein c, nämlich c’, mit der Frequenz 4×138 Hz.

Abb. 1-2

Diese sog. Obertonreihe entsteht überall in der Natur, wenn man z.B. ein ventilloses Horn anbläst, oder den Flageolett-Tönen auf einer Gitarrensaite nachhorcht, aber auch bei den Heulschläuchen, die unsere Kinder über ihren Köpfen wirbeln.

Aus der Obertonreihe ergeben sich folgende Intervallproportionen:

Konsonanz
Oktave	1	:	2
Quinte	2	:	3
Quarte	3	:	4
Große Sexte	3	:	5
Große Terz	4	:	5
Kleine Terz	5	:	6
Kleine Sexte	5	:	8

Dissonanz
Kleine Septime	5	:	9
Große Sekunde	8	:	9
Große Septime	8	:	15
Kleine Sekunde	15	:	16
Tritonus	32	:	45

Zwischen dem ersten und zweiten Ton der Obertonreihe entsteht also eine Oktave = (1:2), zwischen dem fünften und achten Ton eine kleine Sexte = (5:8) usw.

Sofort fällt eine Grundregel auf:
Je niedriger die Zahlenverhältnisse, umso stärker die Konsonanz, d.h. umso harmonischer der Zusammenklang. Die gestrichelte Linie gibt in etwa an, wo konsonante Klänge in dissonante übergehen.

Abb. 2  ←Zurück

Zum vergrößern auf das Bild klicken. ←Zurück

Abb. 3 ←Zurück

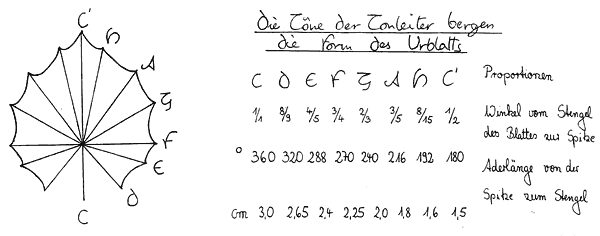
Fussnote 1
Der einfachste Fall eines rechtwinkligen Dreiecks, das den Lehrsatz erfüllt, ist ein klassisches Beispiel der Harmonik, nämlich das Dreieck mit den Seitenlangen 3, 4 und 5 (die Summe der beiden Kathetenquadrate, 9 + 16, ergibt als Hypotenusenquadrat 25. Die Töne 3, 4 und 5 der Obertonreihe ergeben den Dur-Dreiklang, die Saiten im Verhältnis 3 : 4 : 5 ergeben den Moll-Dreiklang. ←Zurück

Fussnote 2
Die Zahl 5 ist in vielen Kulturen ein Symbol der Liebe, des Eros, der Geschlechtlichkeit. So ist der 5. Wochentag der Venus oder Freia (veneris dies, vendredi, Friday, Freitag) gewidmet, Hellenistische Tempel der Liebesgöttin hatten vielfach einen fünfeckigen Grundriß and in der Astrologie gehört die Liebe in das 5. Horoskop-Feld. ←Zurück